프로그래머스 Level 2 - Summer/Winter Coding (2019) - 멀쩡한 사각형

문제 설명

가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다. 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상태이기 때문에, 이 종이에서 원래 종이의 가로, 세로 방향과 평행하게 1cm × 1cm로 잘라 사용할 수 있는 만큼만 사용하기로 하였습니다.
가로의 길이 W와 세로의 길이 H가 주어질 때, 사용할 수 있는 정사각형의 개수를 구하는 solution 함수를 완성해 주세요.

제한사항

• W, H : 1억 이하의 자연수

입출력 예

WHresult

8

12

80

입출력 예 설명

입출력 예 #1
가로가 8, 세로가 12인 직사각형을 대각선 방향으로 자르면 총 16개 정사각형을 사용할 수 없게 됩니다. 원래 직사각형에서는 96개의 정사각형을 만들 수 있었으므로, 96 - 16 = 80 을 반환합니다.

 

---

문제 설명을 읽는데 묘하게 예전에 구글링으로 해설을 봤었던 느낌이라 기억을 더듬으며  최대공약수를 생각해내었다.

그런데 문제는 최대공약수를 이용하여 어떻게 답을 도출해낼지 감이 잡히지 않았다.

그래서 다시 한번 구글링을 하여 설명을 읽어보았다...

 

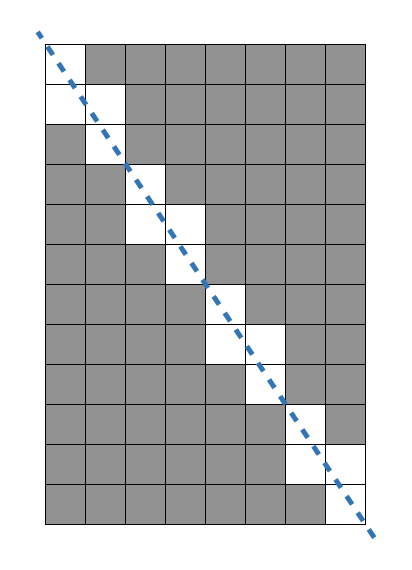
1. 대각선이 빨간색 꼭지점에 닿일때 마다 파란색 동그라미 안 테트리스 모양이 반복 된다.

2. w 는 2칸 h 는 3칸 씩 늘어날 때 마다 반복된다.

3. 최대공약수 4 의 2배 , 3배이기 때문이다.

4. 전체 사이즈 - ((( 가로 / 최대공약수) + ( 세로 / 최소공배수 ) - 1 ) * 최대공약수)

5. 가로 와 세로의 사이즈가 같은 노란 형광색 부분이 있기 때문에 -1을 해준다.

 

아래는 코드 입니다.

 

import java.util.*;

class Solution {
    public long solution(int w, int h) {
        long answer = 0;
        
        long entire = (long)w * h;
        
        // 더 큰 값으로 나누어주어야해서 min max 구분
        long gcd = gcd(Math.min(w,h) , Math.max(w,h));
        
        return entire - (((w/gcd) + (h/gcd) -1)  * gcd);
    }
    
    // 최대공약수 구하는 함수
    public long gcd (long w , long h){
        if(h == 0){
            return w;
        }
        return gcd(h , w%h);
    }
    
}